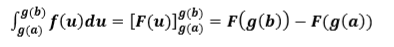Kalkulus 2

Assalamualaaikum  wr.wb, Pada postingan kali ini saya akan membahas dan menjawab soal latihan untuk materi tentang integral parsial tentu.      Rumus atau aturan pada integral parsial tentu sama dengan materi pada pertemuan 12 yaitu pada integral parsial tak tentu. Hanya saja pada integral parsial tentu dimasukkan batas atas dan batas bawahnya setelah fungsi integran diintegralkan. Latihan Soal PEYELESAIAN Demikian soal dan jawaban dari materi pertemuan 13 tentang integral parsial tentu. Terimakasih sudah mampir di blog ini. Jangan lupa tinggalkan jejak. Terimakasih💖💖

Assalamualaikum Berikut adalah soal dan penyelesaian dari materi integral parsial tentu. Silahkan baca materi pembahasan integral parial tak tentu  di sini . Untuk no 1-7 saya menggunakan cara ke 1 sedangkan 8-10 saya menggunakan cara ke 2. LATIHAN SOAL PENYELESAIAN Terimakasih sudah mampir diblog ini. Semoga dapat bermanfaat dan jangan lupaa kritik sarannya

        Assalamualaikum, kembali lagi di pembahasan materi kalkulus 2. Pada post kali ini saya akan membahas integral parsial tak tentu. Langsung saja yaaaa       Integral parsial merupakan suatu Teknik pengintegralan yang digunakan jika persoalan integral tidak bisa diselesaikan menggunakan aturan dasar atau aturan substitusi (Hass,Weir,George B.Thomas,&Hell,2016). Disebut juga metode substitusi ganda. Dalam pengoperasiannya harus dimisalkan dengan u dan dv. Harus menentukan du(turunan dari fungsi u) dan v(integral dv). Rumus yang digunakan adalah :      Dalam menyelesaikan persolan integral dengan aturan integral parsial terdapat dua metode atau cara yaitu : 1.        Cara 1 a.        Ubah soal ∫ f(x) dx menjadi  ∫  u dv b.       Tentukan nilai du (turunan dari u) dan tentukan nilai v(turunan dari v) c.        Masukkan hasil langkah 1 dan 2 ke dalam rumus baku integral parsial 2.       Cara 2 a.        Ubah fungsi integran menjadi bentuk  ∫  u dv , sehingga diperoleh f

    Asslamualaikum :)  pada blogpost  kali ini akan dibahas materi dan latihan soal  mengenai   Integral fungsi rasional.                              Fungsi rasional adalah suatu fungsi yang dinyatakan dalam bentuk 𝐹(𝑥) = 𝑓(𝑥)/ 𝑔(𝑥) ,  dimana f(x) dan g(x) adalah fungsi aljabar suku banyak (polinom) dengan  syarat derajat polinom pembilang lebih kecil dari penyebut dan g(x) ≠ 0.       Fungsi rasional dibagi menjadi 2 macam, yaitu:  a. Fungsi Rasional Sejati       Fungsi rasional sejati adalah fungsi rasional yang derajat polinom pembilangnya lebih besar daripada derajat polinom penyebutnya. (E.Vaberg, Purcell, & Rigdon, 2007)  b. Fungsi Rasional Tidak Sejati       Fungsi rasional tidak sejati adalah fungsi rasional yang derajat polinom pembilangnya lebih besar atau sama dengan derajat polinom penyebutnya. (E.Vaberg, Purcell, & Rigdon, 2007)            Dalam menentukan integral fungsi rasional, langkah yang ditempuh adalah:   a. Nyatakan integrannya dalam bentuk fungsi ra

Assalamualaikum Wr.Wb, pada blogpost kali ini akan dibahas materi dan latihan soal mengenai  aturan substitusi integral tentu fungsi eksponensial. Fungsi eksponensial adalah invers dari fungsi logaritma natural (ln), yang dapat ditulis:     y = ln x  ↔  x = e^y Fungsi logaritma dapat didefinisikan sebagai kebalikan (invers) dari fungsi eksponensial.Secara umum, fungsi logaritma natural dari x ditulis ln x (dibaca len x).                                       Teorema yang digunakan adalah : Untuk ln 1 = 0, maka e^0 = 1  Untuk ln e = 1, maka e^1 = e  Untuk ln 1 /𝑒 = -1, maka e^-1 = 1/ 𝑒 Untuk ln e^2 = 2, maka e^2 = 2                           Sehingga dari permisalan tersebut dapat diperoleh teorema bahwa:    y = ln x jika dan hanya jika x = e^y Sifat-sifat fungsi eksponensial  e ^ln x = x, untuk semua x > 0, x ∈ R  ln (e^x) = x, x ∈ R                Rumus atau aturan yang digunakan dalam integral tentu fungsi eksponensial sama dengan pada integral tentu yang telah di jelaskan pada

Assalamualaikum Wr.wb. pada kesempatan kali ini saya akan membahas materi dan latihan soal dri aturan substitusi integral tak tentu fungsi eksponensial.        Sebelum membahas integral fungsi eksponensial, perlu diketahui terlebih dahulu mengenai definisi dari bilangan eksponensial. Konsep dari bilangan eksponensial ditemukan oleh ahli matematika asal Swiss, Leonard Euler.     Bilangan eksponensial merupakan suatu bilangan irrasional yang dilambangkan dengan huruf e yang berasal dari bilangan Euler, yaitu sebuah bilangan yang merupakan nilai pendekatan dari bentuk (1 + 1 /𝑛 )^ 𝑛  (pangkat n).      Untuk mengetahui integral fungsi eksponensial perlu diketahui terlebih dahulu t urunan dari fungsi eksponensial berikut.  Dari turunan tersebut dapat disimpulkan bahwa integral fungsi eksponensial dapat ditulis:  Dengan menggunakan aturan substitusi maka bentuk dasarnya adalah sebagai berikut : Langkah-langkah Menyelesaikan Integral Tak Tentu Fungsi Eksponensial      Untuk menyelesaikan pe

Assalamualaikum W.r.Wb. pada postingan kali ini akan membahas materi dan  latihan soal  tentang aturan substitusi integral tentu fungsi trigonometri.      Integral tentu fungsi trigonometri merupakan integral tentu dengan interval tertutup [a,b] pada fungsi trigonometri. Penggunaan aturan substitusi integral tentu pada fungsi trigonometri memiliki perbedaan dengan penerapannya pada fungsi aljabar. Perbedaannya terletak pada:  Integral tentu fungsi trigonometri umumnya menggunakan interval 𝜋 radian, sehingga untuk menentukan penyelesaiannya harus mengubah interval tersebut menjadi interval baru dengan bentuk bilangan real;  Pangkat dari fungsi integran pada aturan substitusi integral tentu fungsi trigonometri umumnya lebih dari 1, negatif, atau pecahan; Pada beberapa kasus fungsi integran yang memiliki sudut ≠ x, seperti 2x, 3x, 4x, dst,  Untuk  aturan substitusi integral tentu fungsi trigonometri berlaku :      Aturan rantai fungsi trigonometri didefinisikan sebagai salah satu metode

Assalamualaikum W.r.Wb. Pada kesempatan kali ini saya akan membahasa materi dan latihan soal tentang  Aturan substitusi integral tentu fungsi aljabar      Untuk menyelesaikan soal-soal integral dapat diselesaikan jika sudah mempunyai bentuk yang sesuai dengan rumus dasar .jika belum maka harus diubah dengan aturan substitusi .      Adapun rumus aturan substitusi untuk fungsi aljabar adalah sebagai berikut :        Untuk menentukan aturan substitusi substitusi integral tentu fungsi aljabar juga berlaku sebagai berikut :                       Aturan substitusi integral tentu akan berbeda dengan aturan substitusi interal tak tentu.Pada aturan substirugi interval yang diberikan tidak mengalami perubahan , maka pada aturan substitusi integral tentu akan mengalami perubahan , yang semula a≤x≤b menjadi g(a) ≤u≤g(b)   Langkah-langkah menyelesaikan soal integral tentu dengan aturan substitusi 1.pastikan fungsi integran berbentu dasar integral [g(x)^r g’(x)dx. Jika belum harus di