Pertemuan 12 : Integral Parsial Tak Tentu
1.
Cara 1
a. Ubah soal ∫ f(x) dx menjadi ∫ u dv
b. Tentukan
nilai du (turunan dari u) dan tentukan nilai v(turunan dari v)
c. Masukkan
hasil langkah 1 dan 2 ke dalam rumus baku integral parsial
2.
Cara 2
a. Ubah
fungsi integran menjadi bentuk ∫ u dv , sehingga diperoleh fungsi u dan
dv
b. Tentukan
turunan dari fungsi u hingga bernilai 0 dan integralkan dari fungsi dv sampai
u bernilai 0 dengan menggunakan aturan table turunan dan integral :
c. Hasil
integral diperoleh dengan menjumlahkan perkalian u dengan integral pertma dv
kemudian mengurangkan perkalian du dengan integral kedua dv. (jika u=0 didapat
lebih dari 2 kali turunan, maka pada perkalian fungsinya gunakan pola penjumlahan,pengurangan,penjumlahan,pengurangan, dan seterusnya).
Untuk
fungsi integral yang memuat fungsi In tidak bisa diselesaikan dengan cara kedua.
Contoh soal dari integral parsial tak tentu :







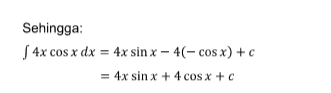
Komentar
Posting Komentar