Tugas Pertemuan 5 : Integral tentu fungsi aljabar
Asalamuaikum, pada kesempatan kali ini saya akan membahas materi dan latihan soal tentang Integral tentu fungsi aljabar
Penjumlahan Riemann dijadikan dasar untuk menentukan konsep dari integral tentu, baik untuk integral tentu fungsi aljabar, trigonometri, maupun ekponensial. Penjumlahan Riemann merupakan salah satu metode untuk menentukan luas daerah yang dibatasi oleh kurva pada interval tertentu dengan menggunakan pendekatan nilai luas beberapa persegi panjang sebagai interval-interval dari luas daerah yang dicari.
Integral tentu atau sering disebut definite integral merupakan limit dari penjumlahan Riemann sebagai perumuman dari konsep luas suatu daerah. Misalkan f merupakan fungsi yang terdefinisi dalam interval tertutup [a,b] yang dapat dilakukan penjumlahan Riemann, maka secara geometri fungsi tersebut dapat menyatakan jumlah luas persegi panjang
Andaikan f kontinu pada interval [a,b] dan andaikan F merupakan sembarang anti turunan dari f, maka berlaku integral tentu sebagai berikut.
- f(x) : fungsi integran
- dx : variabel integrasi
- F(x) : hasil integrasi
- a : batas bawah variabel integrasi
- b : batas atas variabel integrasi
- F(a) : hasil integrasi untuk batas atas
- F(b) : hasil integrasi untuk batas bawah
Untuk mengaplikasikan rumus tersebut pada persoalan integral, harus diperhatikan sifat-sifat integral tentu berikut.
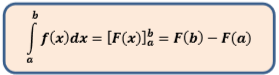
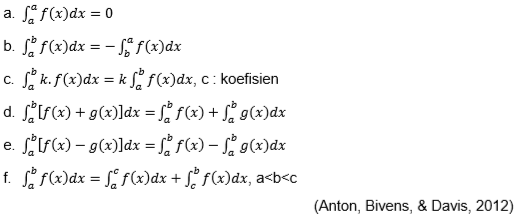



Komentar
Posting Komentar