Tugas Pertemuan 7 : Aturan substitusi integral tentu fungsi aljabar
Untuk menyelesaikan soal-soal integral dapat diselesaikan
jika sudah mempunyai bentuk yang sesuai dengan rumus dasar .jika belum maka
harus diubah dengan aturan substitusi .
Adapun rumus aturan substitusi untuk fungsi aljabar adalah
sebagai berikut :
Untuk menentukan aturan substitusi substitusi integral tentu
fungsi aljabar juga berlaku sebagai berikut :
Aturan substitusi integral tentu akan berbeda dengan aturan
substitusi interal tak tentu.Pada aturan substirugi interval yang diberikan
tidak mengalami perubahan , maka pada aturan substitusi integral tentu akan
mengalami perubahan , yang semula a≤x≤b menjadi g(a) ≤u≤g(b)
Langkah-langkah menyelesaikan soal integral tentu dengan
aturan substitusi
1.pastikan fungsi integran berbentu dasar integral [g(x)^r g’(x)dx.
Jika belum harus diubah
2.Misalkan bagian fungsi integran yang berpangkat menjadi
fungsi u
3. Turunkan fungsi u sehingga diperoleh du=dx
4.Nyatakan nilai dx agar sesuai dengan soal . kemudian
substitusikan pemisalan tadi ke integral semula
5.Tentukan interval baru dengan mensubstitusikan interval
[a,b] ke dalam fungsi u
6.Ubah
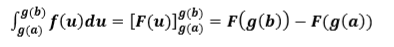







Komentar
Posting Komentar